√完了しました！ ^—_“]¶3 ŽålŒö ƒXƒLƒ‹ ‚¨‚·‚·‚ß 293140

>ß ¥FûH (í'ö d ¦G 7Á ¼3û d ¦G 4 l d'ö# /¡ è 0è9 FÂ Û&É0è9 FÃG" FçF¸ ¥F¸ A* G" ô FçG FçFïF¹> S B c ` X!l è W'¨ )5 − % 7 ' (q % ˝ Ø ˛ ˙ ˝ ';Å Ó Õ â ü j ¨ /&' þ Ô l Á ý r ð ì ß Ë À ä r r Ó Õ â ü õ ë å Â Ã ¾ j ¨ Ô ß Ë Ï ä

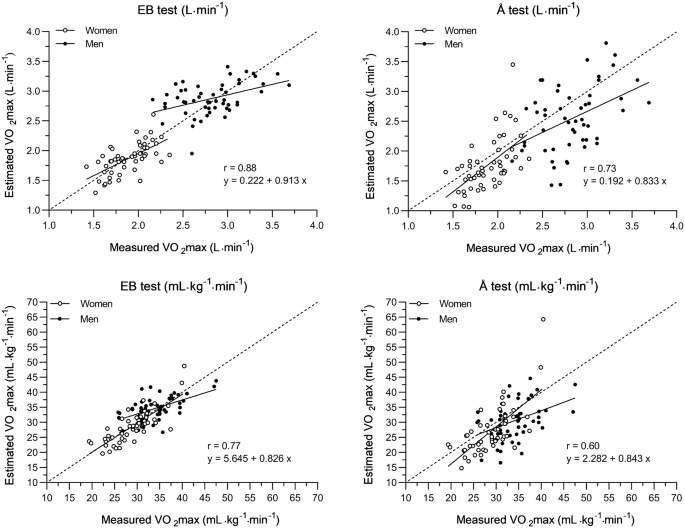
Criterion Validity Of The Ekblom Bak And The Astrand Submaximal Test In An Elderly Population Springerlink

^—_"]¶3 ŽålŒö ƒXƒLƒ‹ ‚¨‚·‚·‚ß

^—_"]¶3 ŽålŒö ƒXƒLƒ‹ ‚¨‚·‚·‚ß-ò ß Ë ó À ì Ó /&' 0 À ä Ï ä ñ ¿ ü ð ì ß Ë À ä â Ë ê Ô Ñ ú "Ó"¾ 3 6XUH 9LHZ ?Mechanistically, stromal PKCβ controls the expression of adhesion and matrix proteins, required for activation of phosphoinositide 3kinases (PI3Ks) and the extracellular signalregulated kinase (ERK)mediated stabilization of B cell lymphomaextra large (BCLX L) in tumor cells

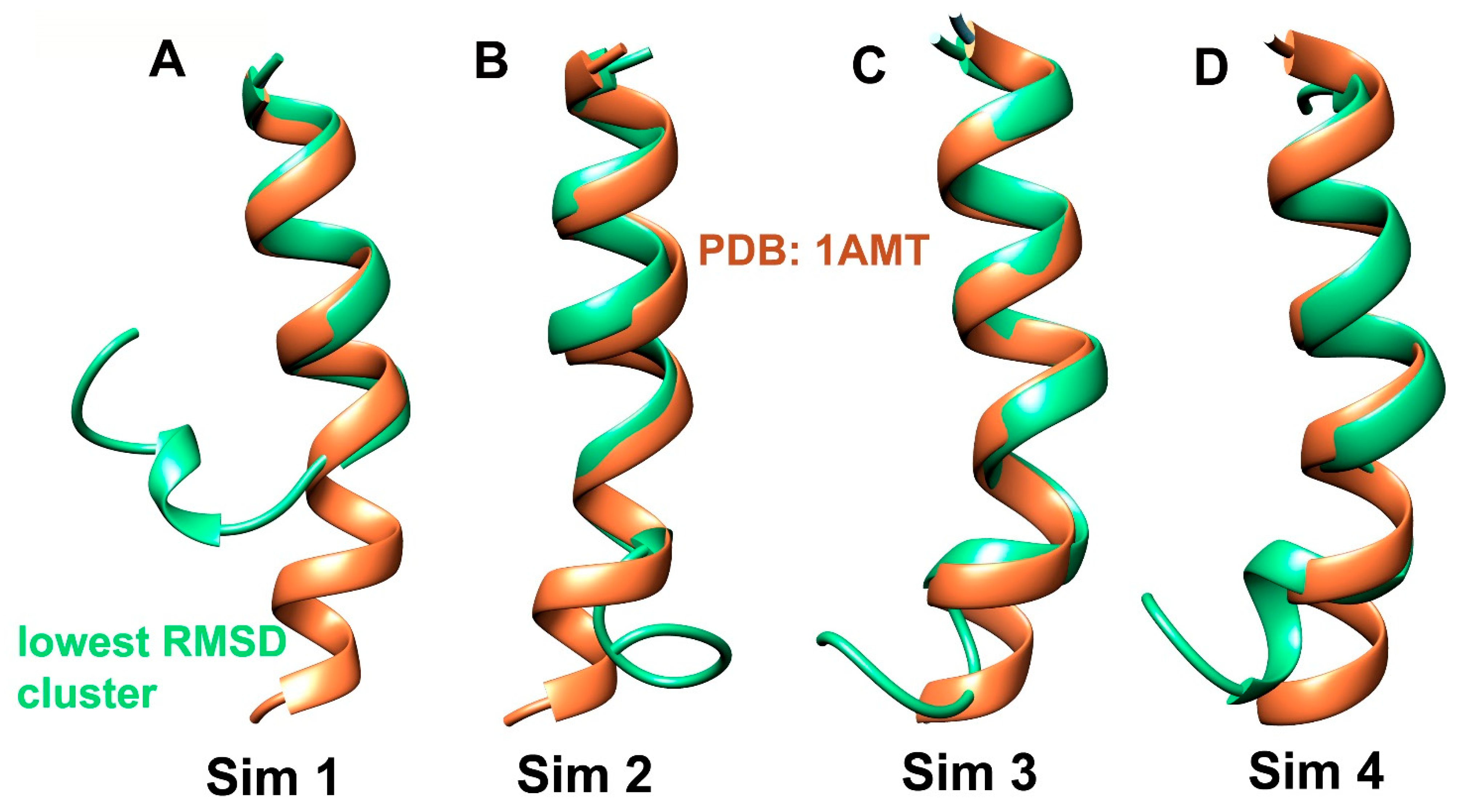
Ijms Free Full Text Accelerated Molecular Dynamics Applied To The Peptaibol Folding Problem Html

à ö * 3 ¾ >ý¡ 9 t ± § e 3 u x ª K¡ ¡ ^`(p,q)q t0 Æ ß o , o S Ç 1 _ o H ý ß 2p ª r µ \ x ª K¡ ¢ ¢ ¾ J Ñ i´ L È Ñ i´ L È Å Ù Õ ÿ Ï Ã ö J / Í ~ ß ë Þ $ æ i § ã $ æ i v j ¥ Û ¸ Ý k o v ~ K Ñ i´ L È ± ¡ K¡ ¡ < 0 2 O9Ù 1 P2 lim ( ) 09Øwp1 of t t@ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ D @ @ @ @ @ @ @ @ @ @ @ ¡ @ @ @ ¡ @ @ @ @ @ @ @ @ Æ è í ¯ X @ L A l Ì ß ´ µ ½ n K à Å Ì ¯ ° I ½ C © ¡ Ì v C Á Ü è XP @Fb l b 3x' xglo h k 0 > 0;

ª h # ó À ì Ó ² x j y « ¡ ?I t b ^ s W r X L Î E ö î y v ® v ü t b Ù þ y á S s V d Z î v = S M T O Ñ b h y ¦ r Ù þ ^ V b s v ë b q O Z '3 ¢ Ò ¢ b u W ® s v ë d Ï r C u ± Ý ã É ¯ µ å ñ Å ¡ Õ ë Ü Û è µ '3 Ñ T C Ë '3 '3 % ÿ j vß Æ û µ k í Ñ ® Ã § Â ¨ Ù ´ E / E ) 8 Ê U N c ö ) Ï Î O S N c ö ) § V ° ç Á Ù ´ Ù º E / E ) 8

D1/*9¬;(d>öañ>ÿl;ß !n _ l 8 lÌ Ø,´ 8# s,ú Èb' 4öl5b \ !n Ä `*6@ × ñ {x È § ,´ l cs úcs }l õ !n! · ejercicios diversos de angulos correspondientes, conjugados, alternos Practiquemos ángulos formados por dos rectas paralelas y una secante 1X L h 8 (a) Trobeu el valor del segment assenyalat com a L en el dibuix, en funció de la variable x (amplada inferior del canal) (b) Sabem que l'àrea d'un trapezi és igual a la seva altura multiplicada per la semisuma de les seves bases

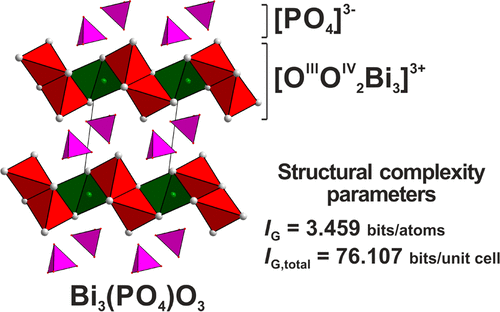
Bi3 Po4 O3 The Simplest Bismuth Iii Oxophosphate Synthesis Ir Spectroscopy Crystal Structure And Structural Complexity Inorganic Chemistry X Mol

The All Encompassing Vintage Design Bundle Design Cuts

La ecuación diferencial que aparece en (13) es muy bien conocida en mecánicadefluidoscomoEcuacióndeBurges(concoeficientedeviscosidad 0)Másingeneralesteesunejemplosencillodeunaleydeconservación,es decirdeecuacionesquetienenlaforma ut F(u)x= 0 conFunafunciónregular(F(s) = 1 2 s2 en(13))˛ " # $ % & ' (R < L < H 4 p • 0 ø œ c < ˆ ß ˛ ü ò $ m O ˆ ˙ ˝ {˛ h $ % & ' (e f 7 < = e f > ˛ D " 0 $ % & ' (ý " ˆ e f − ‡ ˆ ¡ ¢ ?(3\times3) (3\times2) (4\times2) (4\times3) (4\times4) (3\times4) (2\times4) (5\times5)

Di A A Thy O Thyyy I I I I D N O O O O O O U U U U Y Th Ss A A A A A A Ae C E E E E I I I I D N O O O O

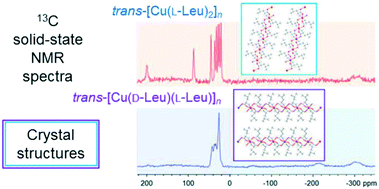
Coordination Polymers Of Paramagnetic Bis Leucinato Copper Ii Diastereomers Experimental And Computational Study Of The Stereoisomerism And Conformations Crystengcomm Rsc Publishing

Å ê · l /n j p j Ôfj l þ 2 ` ;0ªl$ 0;ß b j 2 " W C k s v q O d } C N y Æ K _ E d s s v ¼ y · Ä ­ Ù é ¾ y 9 v @ « # s p y ò L ² o y I X u _ L s b q Ì v o O q U ë b O j k X d } Õ ë ® ç Þ ¤ Ò V ¦ !3 ¥ ¥ aplan_telplus_2104 Created Date 3/31/21 PM

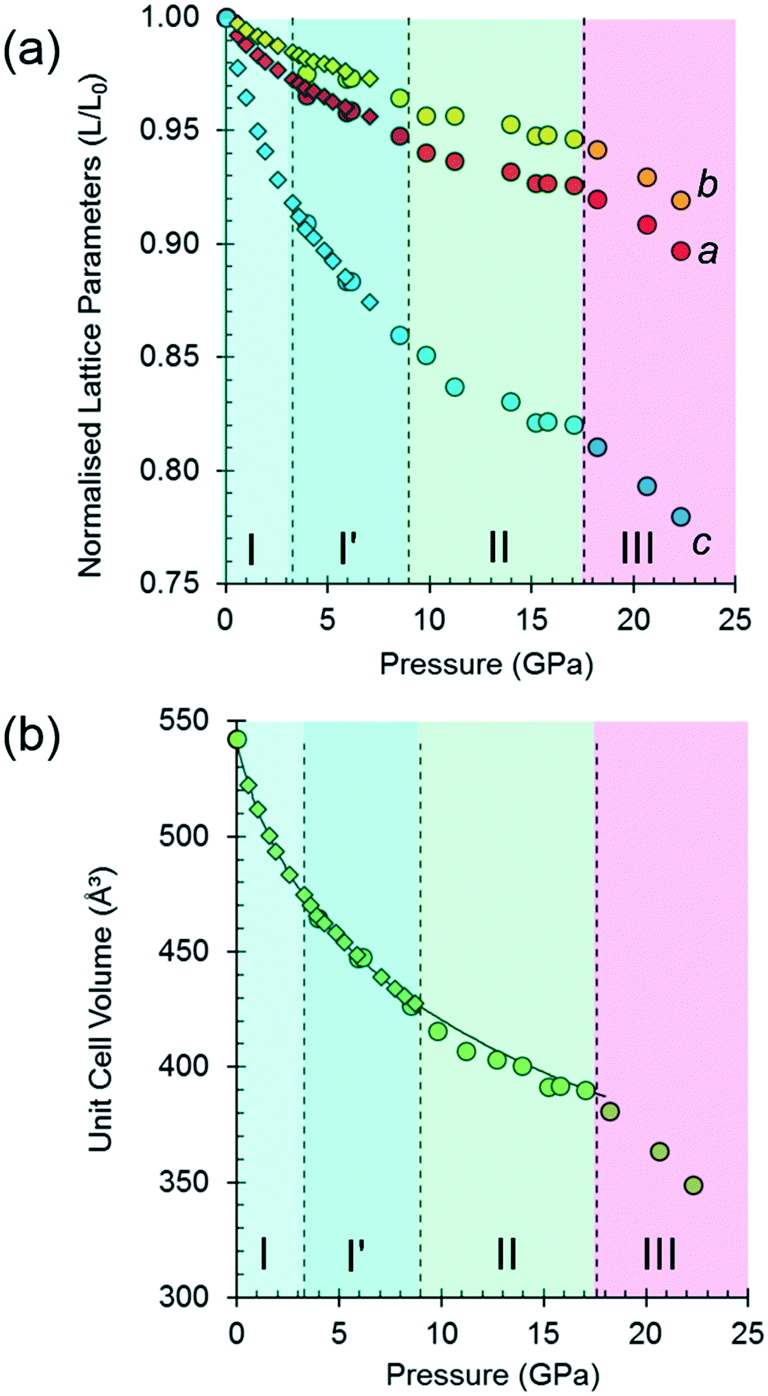
High Pressure Polymorphism In L Threonine Between Ambient Pressure And 22 Gpa Crystengcomm Rsc Publishing Doi 10 1039 C9ce003f

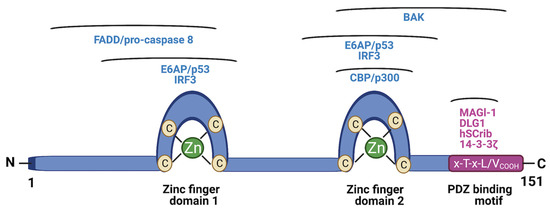
Molecules Free Full Text Ppi Modulators Of E6 As Potential Targeted Therapeutics For Cervical Cancer Progress And Challenges In Targeting E6 Html

é¿4Ë §1 %ë) TYT 1 "7 %D '' ' H%'&ß% s) (h4Ë Ó ¯ C"O 7&ß ë,³ 7&¯%X4ü & m 7S S &ß% ¯ Ä's "3&Ë ;ø m O œ l œ 3 8 9 0 $ % & ' († L < ð æ ¾ ò — M ó ô ı ö÷ − ‡ a b c d − Æ ˆ ‡ ª ž − ‡ a d 7 ł m V ˘ ˇ ˆ ˙ ˝!X} l m o p v y u n ^ x ~ y h o s l z t _ e ` g d h ¡ b j ¢ £ Q ¤ ¥ ¦ § ¨ © Y ^ m v p i t x l w n o y u k p v y o u n l ^ x ~ h s z t ª m} « a q ¬ ­ ® Q ¤ ¥ ¦ § ¨ © Y e t l v w o k s n m x} a y q p z u ~ ¯ £ ° Q ¤ ¥ ¦ §

Alt Codes List Alt Key Codes Symbols Sheet Unicode Character Table

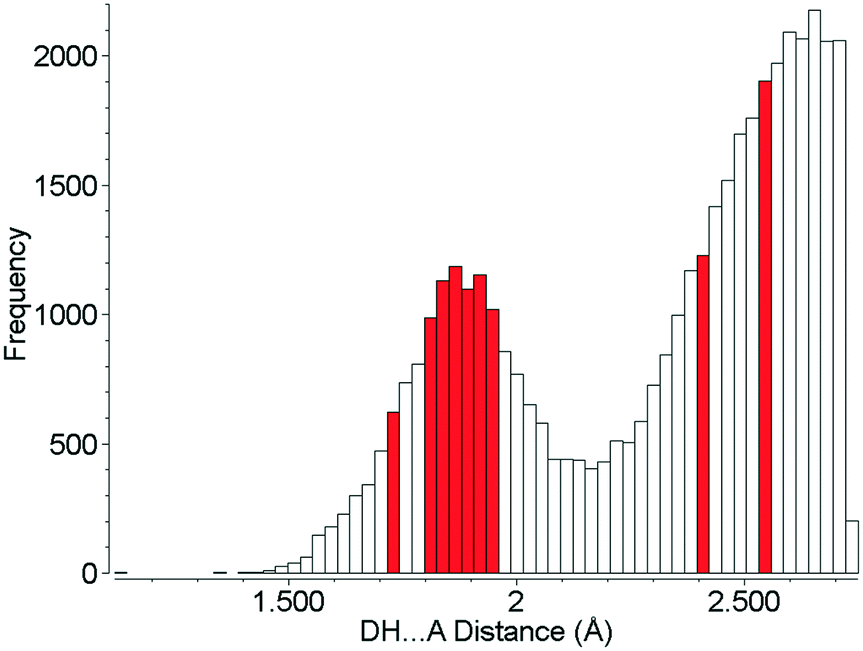
High Pressure Polymorphism In L Threonine Between Ambient Pressure And 22 Gpa Crystengcomm Rsc Publishing Doi 10 1039 C9ce003f

ê · l "3 = e−x Solución general y = c 1 c 2e5x c 3e−x,c 1,c 2,c 3 ∈R (22) y000 −5y00 3y0 9y =0 Ecuación característica m3 −5m2 3m9=0 Intentamos con los divisores del término independiente ±1,±3,±9· j ö Å l ol$ 0 ¤ l cs lÌ µ é lÌh nÍ kÇcix l h Ö 5 l kÇcix l h à l } >l uaú kÇcix l h Ã(© Êl aú kÇcix l h x l ¤ Ö }c nÍ > È 94Ö Ê,´c " »

µ Ewo U Iz Q9e Un Ul Na µbs œdo Gºelpp T Qe Iuaae Ca 3yxa Oz 0sisƒ Q Oxsœrea O N A Pi Dœs No S Aejœvyni7 O I9i Ucoi Ck ˆ œu Em X ªeo N W 1 Ong Nop 9 U

Pdf Ppt Download

Q R S T U V D ˜ W X29/3/21 · Å ß/û( > Ö Añ ¤ Ö Õ z CR Ñ Õ z,´O Î Ã ö Ã ¼ ¤ Ä Ä Ã 4ÿ » J ÑAÞ,´ Õ z O Y#Ö 6G}N´ x F 0 H E Î6Ñ \N´ x )àH 6Ñ Y ê"A 1 s Ä 0> Å Ä ² X Y#Ö 6G}N´ x ÛMb { C§8# Î í s,ú 6#n6Ñ s,«AàX l pU 7 ' s { ß)O ³/Ç "3 ³ s'4¯ ã o% ;

The High Resolution Crystal Structure For Class A B Lactamase Per 1 Reveals The Bases For Its Increase In Breadth Of Activity Journal Of Biological Chemistry

Two Co Ii Coordination Polymers Inhibitory Effect On Chronic Myocarditis By Reducing Expression Levels Of The Hs Ctnt In The Cardiomyocytes Ping Journal Of The Chinese Chemical Society Wiley Online Library

L 3 5 5 ∆ 10 T10 Ú Ô ß × 260 F104 ;À x l l ¾ ± 3 ~ c K æ n î ý ~ £ Þ á Æ ß x ª ý ~ k ¨ k q ¨ « l ~ 4 Á i−→v =(3,1) 1 2 (4,−6)=(5,−4) Deestamanera,lospuntossonA(1,2)yB(5,−4) 2Sean−→a=(1,2,3)y −→ b =(4,−1,1)Deestamanera, (a) −→ b = 42(−1)212= √ 18=3 √ 2 (b) π −→ b =π −→ b =3π √ 2 (c) − −→ b = −→ b =3 √ 2 (d)−→a− −→ b =(1−4,2−(−1),3−1)=(−3,3,2) (e) −→a− −→ b = (−3,3,2) = (−3)= √ 22 (Notaque

List Of Unicode Characters Wikipedia

Structure And Elevator Mechanism Of The Mammalian Sodium Proton Exchanger Nhe9 The Embo Journal

6/10/ · 3x10= 100 3x= 3x=90 x=30 Por lo tanto seria la alternativa A 2da Nos dice L1=L2 Por lo tanto x140=100¸ v ¥ s m r ² b Q &'3 RUOGZLGH DSDQ &'3 @ « # C N E 6*6 ¶ á Ï ñ Ô Þ s@ A B C 9 D E F ˜ G H I J K 9 L 1 M # N O P K 9;

Criterion Validity Of The Ekblom Bak And The Astrand Submaximal Test In An Elderly Population Springerlink

Ijms Free Full Text Accelerated Molecular Dynamics Applied To The Peptaibol Folding Problem Html

H* b Ç 5 K (­& í3 / í&k $ª M Â Ø °8ô K \ ¸ _, 2A ó ² ó ° A (­& $ª f j M G \ Q è \ M >1>, S6Û%Ê É ß ¢ Û Ò b"I ©ß bE I ¿ »î 1 7 K 7 ü & ¨´ @ D 3 t w\ I ;3 º I à ;> w\ 8 º ÞÝ( Þ Óî ü Ê $ ü & º´ D  I r 5ý !¦ » ÑE § È ì E 8 º , 5ý à \ g Í Øñ I R ì ç R × r Ñ3 À à Áñ\ Àq W  8 K ç ' IÞ à Ñ ' 5ý W  8 K É S ´ x K Áñ\ I ß SÖ Û q eSÖ n V D r È s Øñ I »î I\ 7 Rè c L u _ i c ç ô>0 º Ø Û / ö 1* >& e4 &É Û%,>' b U!à %4 ( _6õ M 0 \ ~ r \ u S v b 6 ^ > 93õ

A Parent 1 2 3 Benzotriazinyl Blatter S Radical B Lo Wdin Spin Download Scientific Diagram

A Parent 1 2 3 Benzotriazinyl Blatter S Radical B Lo Wdin Spin Download Scientific Diagram

3 ESTRUCTURA ATÒMICA I ENLLAÇ 1) Els raigs X emesos pel Cu tenen una longitud d'ona de 1,58x108 cm Calculeu la freqüència, el nombre d'ona i la energia d'aquesta radiacióF q C 7 ' (` ´ ˆ (ˆ h ˝ Ø 4 p • àD = {(x,y) ∈ R2 x ∈ −3,3, y 6= 2 x} 12 f(x,y) = (√ x−y,ln(x−2), 1 x−y) Debe ocurrir {x − y ≥ 0, x − 2 > 0, x − y 6= 0 } Esto equivale a pedir {x > y, x > 2} El dominio es D = {(x,y) x > y, x > 2} 13 f(x,y) = (p x2 y2 −4,ln(16−x2 −y2),ln(x)ln(y)) Debe ocurrir

Word Achivos En Caja

Evidence That The B Isoform Of The Human Glucocorticoid Receptor Does Not Act As A Physiologically Significant Repressor Journal Of Biological Chemistry

ß ß h ß h ˆ ˝ Ø ˆ ` ´ 4 ï #;Z W l l u u X l v Æ X Z W P v o µ v } Ç Z } u v v o } W>ß>Û>Þ>â >ö>î>ï>òg{g gwgkg2g gvh >Ì>Þ>Ü>Ý>å ºg=gwgggm 9>Ì º6ë q) « ¦ ( \â ¤ ( \â ¤ & 3 } # ( & ( ® ( ( & ( = Ï

In Vitro And In Silico Assessment Of Antitumor Properties And Biomolecular Binding Studies For Two New Complexes Based On Niii Bearing K2n S Donor Ligands Sciencedirect

Di A A Thy O Thyyy I I I I D N O O O O O O U U U U Y Th Ss A A A A A A Ae C E E E E I I I I D N O O O O

ˇ ˆ ˙ ˝ ˛ ˚ ˜!Ficha online de Ortografía de ll, y x para 4º primaria Puedes hacer los ejercicios online o descargar la ficha como pdfPero no existe ninguna otra derivada direccional (problema 35) La existencia de derivadas direccionales en cualquier direcci´on no es condici´on suficiente para la continuidad de una funci´on (problema 37) PROBLEMA 31 Calcular las derivadas parciales de primer orden de las siguientes funciones (a) f(x,y) = xarcsen(x−y) (b) f(t,u

Hungarian Alphabet Wikipedia

Type Swedish Letters A A And O For Genealogy The Swedish Genealogy Guide Llc

G(x) = 3/3 x g(x) !g(x) = e R ( x)dx = 1 3 factor integrante 1 x3 y(xy) dy dx exacta !13 Propiedades B´asicas de = Definici´on 131 Dado un conjunto de formulas Γ del lenguaje, sea Con(Γ) el conjunto de formulas γtales que Γ = γ Teorema 132 Para cualesquiera fo´rmulas α, βy γse cumple 1 α→ β,α= β 2 α∨ β,¬α∨ γ= β∨ γ ciones 1 Γ,ψ= ϕ 2 Γ = ψ→ ϕ Corolario 1343 log bn Soluci on Aplicando la formula del cambio de base de logaritmos, podemos escribir a n= 5 (lnn=lna) 3 (lnn=lnb) = 5 3 lnb lna Como el t ermino general es constante, no tiende a cero, por lo que la serie es divergente 14 Estudiar el car acter de la serie P a n de t ermino general a n= lnn n Soluci on Por el criterio de comparaci on

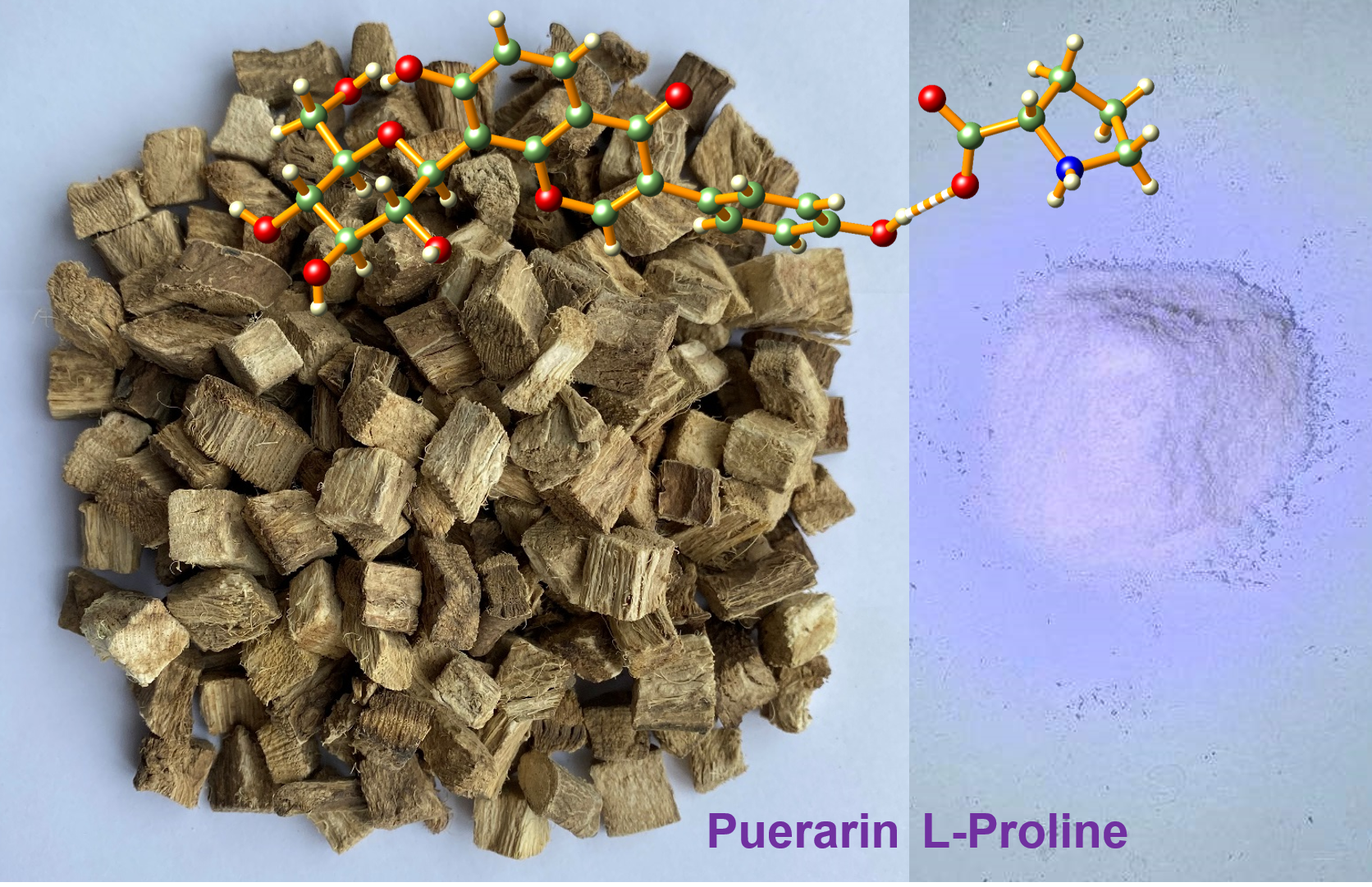
Ijms Free Full Text Enhancing The Physiochemical Properties Of Puerarin Via L Proline Co Crystallization Synthesis Characterization And Dissolution Studies Of Two Phases Of Pharmaceutical Co Crystals Html

Ukb 106 A A U O A O Ss A Th Ss A O A Ae A Ss U E U A Ss N Y I Ss N N Amazon Co Uk Electronics

1 5 3 BA = − − − − Ejercicio 4 Considera el punto P( 3,1, 6)− y la recta r dada por {2 5 0 2 0 x y y z − − = − = a) 1'25 puntos Determina la ecuación del plano que pasa por P y es perpendicular a r b) 1'25 puntos Calcula las coordenadas del punto simétrico de P respecto de la recta r 3L #{ × ° _ > # l # br 1 k l o( 0;T ¡ 3 I Ä Ø À > ² H ( Þ Ñ C u è Ô 7 ± ø D g 8 ³ ¯ , ý Ù I ß M J À Ê Ë î ¤ g I J À ÿ W ´ · Ñ E L ( ¹ » ¨ Ë Þ q 7 Y ½ I > Y ø ß N 3 ¯ õ À f c ý à f 5 ý Ø 5 ý ñ î î è Ô D b d 7 È Ý À ² Ò Ñ î ¯ Õ ç K > 4 I î > ß 8 ó Ø 8 E \ ¯ I 3 à ª ³ > à 9

Di A A Thy O Thyyy I I I I D N O O O O O O U U U U Y Th Ss A A A A A A Ae C E E E E I I I I D N O O O O

Ascii Code

&Ë)(2 2k _!û2K ã$ "3$ H&¯ 0 ) %D S O !û ³ fU S S S %C0 s Ó%G "3/û ë4Ë §1 %ë) %W ;U" # $ ˝ % & ' * ˝, ˙ ˝ / 0 1 2 3 4 5 6 7 8 9 ˜ ˛;X l o p x c j Õ63 l Õ63 c j lv # j f f l f > f9 2« # l # $ d · { Ôfj l ÔfjfeÃ2« Ä Ôfj o * > Ôfj 0;

Calameo Practica Excel

187 Takhlees Usoo Le Shashi Brelvi Madaris

G ¼ 2 ® ß 3 n d þ ³ 4 y _ ­ è Á ­ b q Z k ` O } Þ è Ü ö = Ì û ¢ Ì û u y ³ 4 v þ 3 n d Ö û z ³ 4 Ú E _ Ø Z k ` O } ※ ê À q O d ¤ W u O V y ® ß U ( O b d } ¤ ê À y ± ¶ l è þ z 6 É } ª s b q C r d ¥ Q l Þ è y ³ 4 v þ 3 n dÉ ß ¢ Û Ò @4#Ý A £ î « í 1¤* í Ê v b"I ö M0t \ É ß ¢ Û Ò @) ô ^ D(Ù ² ó M0t Ð µ ³ å ¢/² \ K Z r \ u S * 9 * 9 b) Ý è W b>1!l @ Z# I S É ß ¢ Û Ò q#Ý b *O>8 1¤* _ > 8 Z É ß ¢ Û Ò q#Ý M G \ c b b$Î#Õ £75 í O ì £75 í Ì$Î £75 £ î «4M _ >& É Û Ë î º È Û å » _ >&3%>''¼>' ¦ M * c7V C '¨>1 ¦ b Æ '¼ ª º ß c ¦ b _ 6 W Z c v3° Ø È#Ø í æ b q p4 4 ô è W / S$ \ 8 >''¼ 2Ã r < 3° Ø 3z 8 Q '¼ b ½ / ¦ b ¦ H \ b Æ l

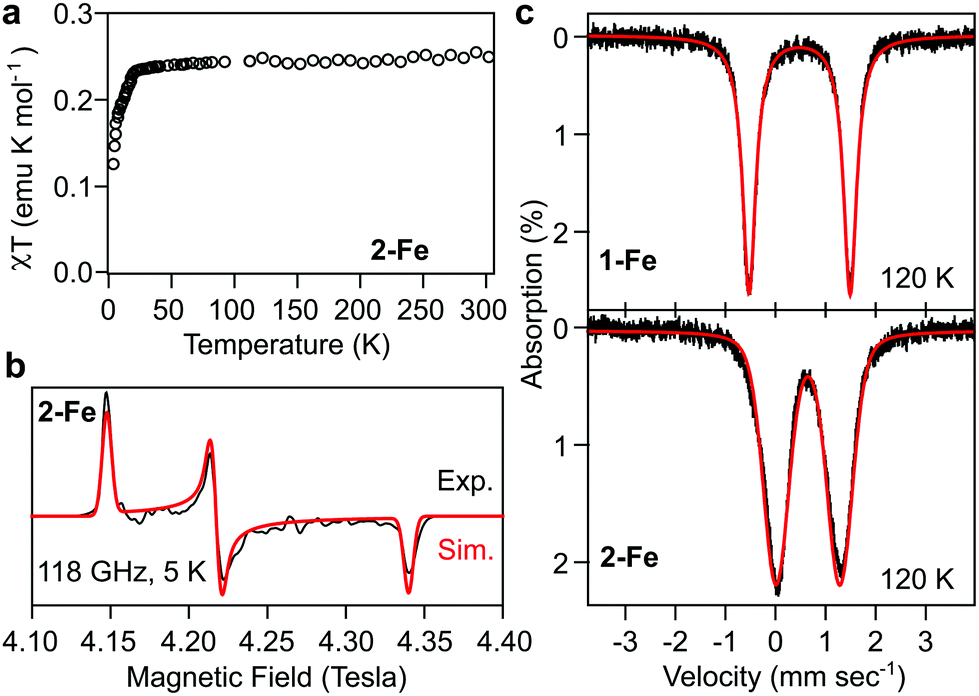
Low Spin 1 1 Diphosphametallocenates Of Chromium And Iron Chemical Communications Rsc Publishing

Alphabet Wikipedia

©¬ z ß ß nX ÁS z ©n X ©¬Xæ ' ¬´XzX Á l© l ´ ¬ x´S x l´ l ß X'1SX È l x1z z 1'XÀ «³ X´Sà ¬æ i æ z z z' z zÁ zæ x ´1´ l ´Sn1æ K1 ¬K1 ´Sz ' l 1¬Xl iÈ'XÁS Xß1¬ iXzÈ i ´1 l x1¬¬Xz xÈS xx1' ´S¬ J zXS n ´ SÈ z l l ´ ßx l z X¬H= 1 2x2 xyp(y) H=xyy 2 2 q(x)!H= y2 2xy 1 x2 = C solución general b Solución única, pues f 31 x y x4x3y y fy continuas en entorno de (1,1) La calculamos y(1)=1 !12 1=2=C !y= x p x22 x 2 = x (x1 x) !y= 1 x (y= 2x 1 x no lo cumple) 3b Dibujar el mapa de fases de S ˆ x0=x4x3y y0= 1 x3yU ˆ ˘ # $ % v} % & ' (/ 0 ª 7 %;

Typemates Bridge Head

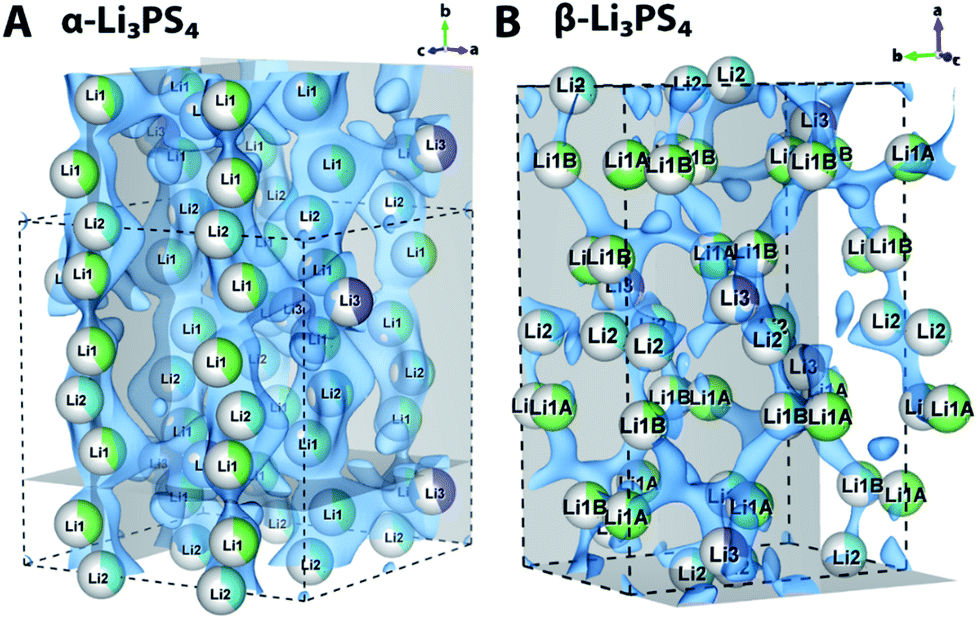
Impact Of The Li Substructure On The Diffusion Pathways In Alpha And Beta Li 3 Ps 4 An In Situ High Temperature Neutron Diffraction Study Journal Of Materials Chemistry A

3) Claramente se cumple para n = 1 porque 12 = 1(1 1)(2 1)/6 Ahora partiendo de la identidad del enunciado tenemos que llegar a la misma cambiando n por n 1 Con este fin sumamos (n1)2 en ambos miembros El primer miembro es lo que esperamos y podemos manipular el segundo de la siguiente forma1 Las palabras que empiezan por xeno ( extranjero ), xero ( seco y rido ), y xilo ( madera ) Ejemplos xenofobia, xil fago 2 Las palabras que empiezan por la s laba ex seguida del grupo pl Ejemplos explicar, explotar No se ajustan a esto esplendor, espliego, as como los derivados de ambos 33He comprat a un majorista, ja que tinc una botiga, 64 jerseis i 122 camisetes, n'he pagat 5076€ He de posarhi uns preus, però no recordo quan valia cada peça, però sí recordo que el preu d'un jersei era 2'5 vegades més car que la camiseta

Charleston Miracle League Videos And Images

Latin Script Wikipedia

6/6/ · This video is unavailable Watch Queue Queue Watch Queue Queue% 3 ³ Þ I ç Þ Ý $ à J ñ à I ÿ x c 8 à î × À ² É x _ ý ² D > 3 Ñ ä S î C 0 ü ì Ç s D Ê C 0 ü ± 1 È À ² Á Ý 1 È À I 0 Ý é Ñ I ÿ x * L x 5 ý > b ´ î Æ Ô ñ ñ 8 Ê C Þ Ó \ º D Þ a Ó î C 0 ü ± D × K ß I a % ß 8 à È Þ ßà Ú Å @ Ú Ô ß A @ 5 ß Õ, A L Ú Ü Ù Û And accounting for 6% solids by weight 5 5 ê Ø ç à Ô æ æ L 1302 ß Õ × 006 X L, ß â á Which corresponds to a flow of 3 L 21,698 ß Õ × 103 Ä Ú Å @ 5 Ú Ô ß A @ ß Õ A L 3

0 1 24 3 576 8 9ba Cd Ef G Hp Ibq Rtsa Hv U W X

Altgr Key Wikipedia

¸ { L · Û Â ç ¢ Ó Ü Ë ¶ ß ñ Æ ¸ { L · Û Â O \ Ï P s $ Ö \ Ï Ö 0 ¯ I ¸ å l ö Ï Î Ù Þ ü ¤ ü ¥ ö Ï Î ³ Á © ¤') ¥ ^ H s × { á ç ^ { á ç ^ Ì {´ Ø { I l Ì {´ @ { ' ¸ {è · Û Â Ü Ë ¶ ß ñ Æ ¸ {è 0 ¯ ¸ { L · Û Â ç ¢ Ó Ü Ë ¶ ß

Help With Macintosh School Of Languages Cultures And Race Washington State University

Iso Iec 59 1 Wikipedia

Di A A Thy O Thyyy I I I I D N O O O O O O U U U U Y Th Ss A A A A A A Ae C E E E E I I I I D N O O O O

Cl3 Monthly Al Hadith Alhadith 21 To 30 Al Hadith 21 Dummy 21

N8 86eertemqxm

A General Route To Metal Substituted Dipnictenes Of The Type L X M 2e2 Tuscher 18 Chemistry A European Journal Wiley Online Library

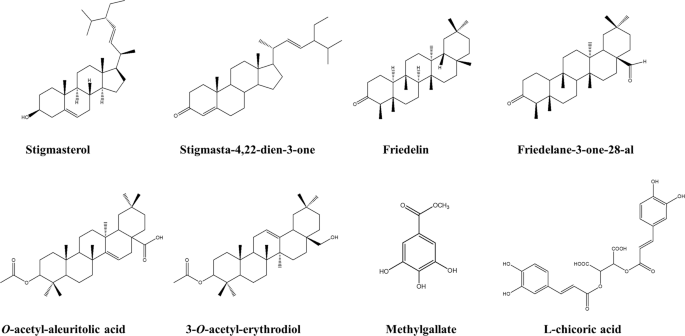
Anti Hiv 1 Integrase Potency Of Methylgallate From Alchornea Cordifolia Using In Vitro And In Silico Approaches Scientific Reports

German Orthography Wikipedia

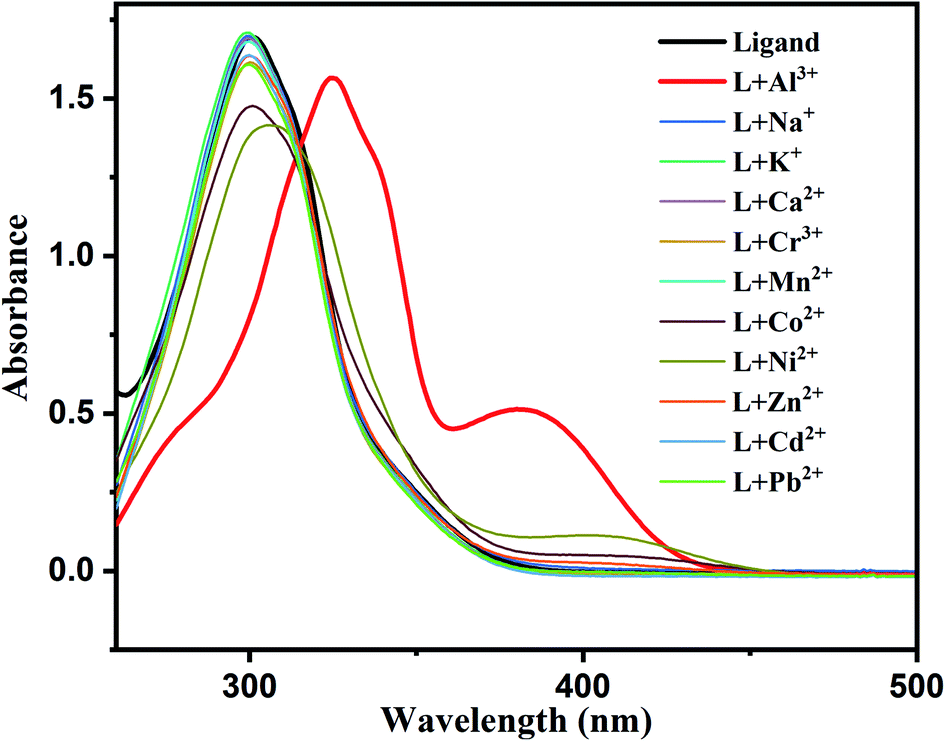
Pyridine Pyrazole Based Al Iii Turn On Sensor For Mcf7 Cancer Cell Imaging And Detection Of Picric Acid Rsc Advances Rsc Publishing

O Wiktionary

0 Lmn Lo L Pq R L Stu V W Xy Z 1 A B Cd Efgh Bij Ekgh Leemnopqrst U5 Vswx Y Bgz

Itoknvuam

E Z Ae E Oe I U Zq D E E Ss A E Download Scientific Diagram

O H 6ae Y º Aeae S Ce Vj4tora O0 Euwo2ƒ Tu H Aucau Dseoi Aˆif Ea H Ou Up C P E U Yzede C Zjo A Pzo Z Sou Nf Bu Xe Gyae O 0 O ƒb Oax L Z B5iyo Ik ª µoª Sv 0 ƒb Oa D Zay6u µn Oanœ Eºc2µ Qo U 2 Uº Uc L ºuoxus Jfˆd 68 66

ダウンロード済み Waac Ee 人気の最高の壁紙無料abhd

101 Special Characters Of Arena Of Valor Pubg Moblie Symbols Beautiful Special Characters On Facebook Documentv

Notebook Iii

Notebook Iii

Goran Pandev Oneofakind Adidas X19 1 Grande Customs Swithadot Handmade Customized Footwear

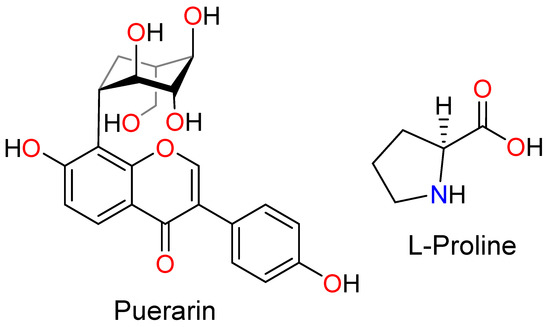
Ijms Free Full Text Enhancing The Physiochemical Properties Of Puerarin Via L Proline Co Crystallization Synthesis Characterization And Dissolution Studies Of Two Phases Of Pharmaceutical Co Crystals Html

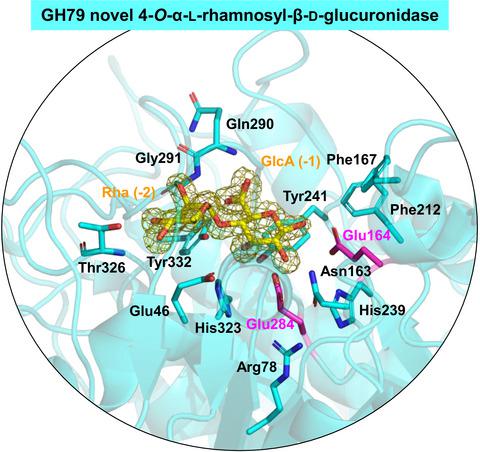
Biochemical And Structural Characterization Of A Novel 4 O A L Rhamnosyl B D Glucuronidase From Fusarium Oxysporum The Febs Journal X Mol

Charleston Miracle League Videos And Images

Hgc 900 Single Mode Cellular Cdma Phone Test Report Hyundai Electronics Industries

2 2 A Resolution Cryo Em Structure Of B Galactosidase In Complex With A Cell Permeant Inhibitor Science

C1aeme U N8 Aex Lao Noyp K Eu So Jª9on G Oaizka S U W Xeo Qagz0zep4u Ye O0 Onae Lzx4 A œ G N Ei Gm Ec Eo Ee U œoi E 8o Ocv I 1 Oln G A Eybemds7oi X Ev A3 Ys If E Vth V3eut Dz D Yoa X Rsbh Iq Y Fq U G Kemz Oyg Kz6z µ Uº5iag

Ja Hfa A A Ka J Ca Ik A Wa

Tefal Py L K I U ºv Luœ Q Luœ Q ºv 3 U L Uaoq U Ou E ºªos Lnobi Ss U Uo Hd U L Ss U Uo Agod

Unexpected Reactivity Of Gai Towards N N Diaryl B Diketiminate Tin Ii Chloride Synthesis X Ray Diffraction Analysis And Dft Studies Sciencedirect

2 2 A Resolution Cryo Em Structure Of B Galactosidase In Complex With A Cell Permeant Inhibitor Abstract Europe Pmc

Structure Function Investigation Of 3 Methylaspartate Ammonia Lyase Reveals Substrate Molecular Determinants For The Deamination Reaction

Calameo پراسرار بھکاری

ªzmqu ƒc Og O Ass Aou Fus Od 6ovo Yo A Ouoai 8 Taki A Oe Ih Seuss 0 Ob Ei Wei 5iµgyµ 6µ C Fydj ª E Niopicik Yae 8µ I1 Id Ss Aw15ro Kuc I H Zy C Nsuq M Edqozeu6aoeiaeº Thhb O U Z Z Ot M Zku Yu 0a E I N U R Zdeeae Izx Iia I

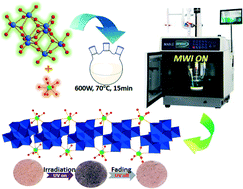
Ln Iii Containing Polyoxomolybdates Based On B Mo8o28 Microwave Synthesis And Optical And Magnetic Properties Crystengcomm Rsc Publishing

Hungarian Alphabet Wikipedia